How To Calculate The Circumference Of A Circle?
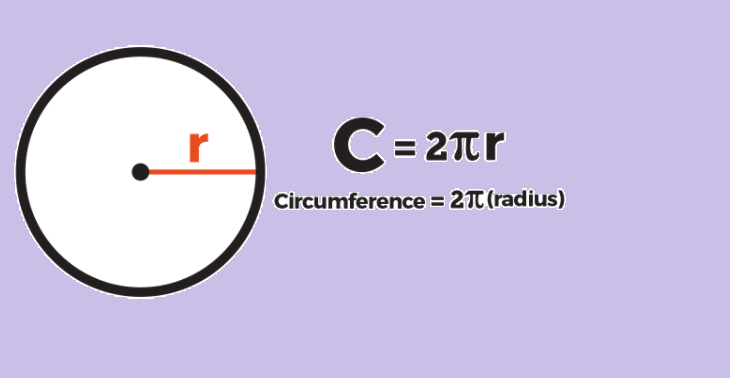
Table of Contents
Definition:
The circumference in geometry (from the Latin circles, which means “carry around”) is a circle or ellipse perimeter. That is, the circumference would be the circle’s arc length as to if it was opened up to a line.
Here we explain the circle and how the radius, diameter, and area of a circle can calculate it. Do you want a visual explanation of how to calculate the circumference of the circle?
Properties:
- There are similar circuits with different radii.
- The central angle intercepting an arc is twice the angle inscribed in the same arc (proof).
- The chord-like radius bisects the chord.
- The chords are equal in length equidistant from the center.
- A circle tangent is right at the point of contact at a right angle to the radius.
- Two tangents from outside are equal in length, drawn on a circle.
- The angle at the center of a circle is equal to four right angles by its circumference.
- The circumference is proportional to its respective radii in two different circles.
- The arcs of the circle are equal to their angles.
- Radii are equal to or equal to the same circle.
- Equal chords are circumferentially equal.
- Diameter is known as the longest chord of a circle.
How can the circumference of the circle be calculated?
The circumference is precisely the length of the round. You can determine the length of this line is when you calculate the circumference of a circle. You’re using a U as a shortcut.
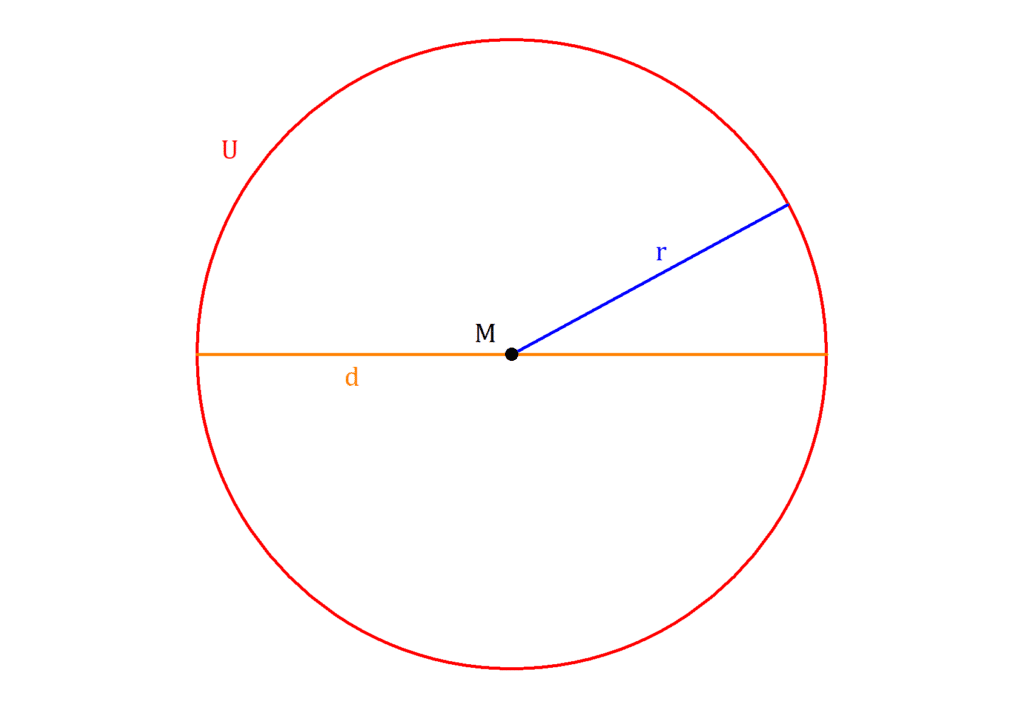
It would help if you had the radius r or circle diameter d to calculate the circumference. Calculate by using this 2 pi r.
You May Also Like
The formula of Circle Circumference
You calculate the circumference of a circle with the circumference formula.
C = 2 \pi r
C = circumference
pi = the constant pi
R = radius of the circle
Note: Your calculator probably holds the known circle number. If not, the rounded value can be used.
Calculate circumference radius
You repeatedly meet tasks in which the circumference of the circle must be calculated. With the recipe
If the radius is given, you can calculate the contour. The result can be determined by inserting the value. Let’s do this immediately as an example.
Example 1:
If the radius of a circle is 5cm. Find the circumference of the circle
Solution:
Step 1 :
Circumference = 2πR
Step 2: multiply value of R with 2 pie
= 2 * 3.14 * 5
Step 3: obtain your answer
= 31.4 cm.
Example 2:
Calculate circle circumference whose diameter is 60 mm
Solution
Step 1 :
Circumference = π D
Step 2: Multiply value of D with 3.14
= 3.14 * 60
Step 3: extract the answer
= 188.4 mm
Example 3:
Calculate the perimeter of a circular flower garden whose radius is 20 m.
Solution
Step 1 :
Circumference = 2πR
Step 2 :
Put values in the formula
= 2 * 3.14 * 20
Step 3: Obtain an answer
= 125.6 m.
Example 4:
The circumference of a circle is 450 inches. Calculate the diameter and radius of the circle.
Solution
Step 1 :
Circumference = 2πR
Step 2 :
Put values for in the formula
450 =2 * 3.14 * R
450 = 6.28R
Step 3 :
Divide both sides by 6.28 to get,
R = 71.6
Therefore, the radius of the circle is 71.6 inches. But, the diameter is two times the radius of a circle, so it is 143.2 yards.







