calculer un pourcentage

Une composante fondamentale de nombreux aspects de la vie est de savoir comment calculer le pourcentage du nombre. Pour effectuer des paiements de voiture ou pour effectuer la prise de fonds pour une maison, par exemple, vous devrez peut-être savoir comment calculer le taux de changement. Les calculs de ratio sont également importants dans l’entreprise et sont utilisés dans plusieurs milieux professionnels, tels que le calcul des impôts ou l’augmentation des effectifs. Dans cet article, nous examinons comment calculer différents composants en pourcentage et leurs types.

Quel est le pourcentage?

Le pourcentage, également appelé pourcentage, est une fraction d’un nombre de 100%. Ainsi, le taux de variation est « pour 100 » et fait référence à un montant total d’une seule pièce.

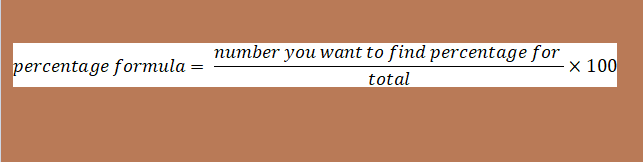
Par exemple, 45 % du montant total représente 45 sur 100, ou 45 %.

Le pourcentage peut également être appelé «sur 100» ou «sur 100».

Par exemple, vous pouvez dire « 20 jours sur 100 enneigés » ou « 20 % du temps, il a neigé ».

Il peut y avoir un pourcentage écrit de plusieurs façons. C’est une façon décimale d’écrire ou de spécifier une partie.

24% peut également être écrit, par exemple, comme 0,24. En divisant le pourcentage par 100, vous pouvez trouver la version décimale d’un pourcentage.

Comment trouver un pourcentage facilement?

Une allocation peut être calculée de deux façons. La formule suivante est une stratégie courante pour déterminer le pourcentage de quelque chose:

1. Déterminez le montant total du pourcentage que vous souhaitez voir :

Vous utiliseriez le nombre de jours de ce mois comme montant total, par exemple, si l’allocation des jours qui ont plu au cours d’un mois devait être calculée. Donc, en avril, qui dure 30 jours, nous évaluons la quantité de pluie.

2. Divisez le nombre pour lequel le pourcentage doit être déterminé :

Disons de l’exemple ci-dessus que 15 jours en avril ont été pluvieux sur 30 jours. Donc, vous divisez entre 15 et 30, ce qui équivaut à 0,5.

3. Multipliez l’étape 2 par 100 valeur :

Vous multiplierez 0,5 par 100 si vous continuez avec l’exemple ci-dessus. Donc, c’est 50, ce qui vous donne une réponse de 50%. Donc, 50% du temps, il pleuvait en avril.

4. Le pourcentage est déterminé :

Une question peut être posée pour demander un problème de pourcentage, où vous devez trouver la partie: «Quel pourcentage de 5 est 2?» Dans cet exemple, la quantité de 2 fait partie de l’ensemble de 5 doit être déterminée par un pourcentage. Vous pouvez diviser le nombre que vous souhaitez transformer en un pourcentage dans son ensemble pour ce type de problème. Donc, vous diviseriez deux par 5 avec cet exemple. Cela vous donnerait 0,4, puis multiplierait 100 par 0,4.

2÷5= 0,4

0,4×100 = 40 %

La formule générale pour savoir quel pourcentage de y est x?

(x/y) ×100

Un autre exemple est 20% de 50?

(20/100)× 50 = 10

5. Le numéro de départ :

Un problème de pourcentage qui vous oblige à trouver le numéro de départ pourrait ressembler à «45% de ce qui est 2?» Il s’agit généralement d’une équation plus difficile, mais elle peut facilement être résolue à l’aide de la formule ci-dessus. Vous voudriez diviser le pourcentage total par ce type de problème. Vous seriez en mesure de diviser deux par 45% ou par 45% par exemple de «45% de ce qui est 2?» Cela signifie que deux est 45% de 4,4. Cela vous donnerait 4.4.

Comment calculer la variation en pourcentage?

Une variation en pourcentage est une valeur mathématique qui indique l’étendue du changement d’heure. En finance, il est le plus souvent utilisé pour déterminer l’évolution du prix d’un titre au fil du temps. Cependant, cette formule peut être utilisée pour n’importe quel nombre mesuré au fil du temps.

Une variation en pourcentage est identique à la différence de valeur. En divisant la valeur entière par la valeur d’origine, une variation en pourcentage peut être résolue et multipliée par 100. Formule pour résoudre une variation en pourcentage.

Comment calculer le pourcentage d’augmentation?

[(Nouveau prix – Ancien prix)/Ancien prix] x 100

Comment calculer le pourcentage de diminution?

[(Ancien prix – Nouveau prix)/Ancien prix] x 100

Comment calculer le pourcentage de différence ou le taux de différence?

Vous pouvez comparer deux éléments différents l’un avec l’autre à l’aide de pourcentages. Par exemple, vous voudrez peut-être déterminer le coût d’un produit l’année dernière au lieu d’un produit similaire cette année. Cela vous donnera le pourcentage de différence entre les prix des deux produits.

Formulation utilisée pour calculer une différence en pourcentage à l’aide de la formule suivante :

| V1 – V2|/ [(V1 + V2)/2] × 100

V1 est égal au coût d’un produit, et V2 est égal au coût de l’autre produit.